이전 강의에서는 선형 시스템을 세우고 Row 와 Column 으로 해석해 보았다
이번 시간에는 선형 시스템의 해를 구하기 위한 방법들을 배워보려고 한다.
이번 강 세부 주제
- Elimination [success case, fail case]
- Back-substitution
- Elimination matrices
- Matrix multiplication
- Elimination [success case, fail case]
우리는 주어진 선형 시스템에 해를 구해야 하는데 이를 구하는 방법이 소거법[Elimination]이다.
(선형 대수를 다루는 모든 소프트웨어는 해를 구할 때 이 소거법을 사용한다고 한다)
예시를 통해 이를 확인하자

이러한 3개 미지수로 이루어진 3개의 방정식이 있다고 하자
(필기한 게 너무 볼품없어 Daum equation editor라는 크롬 extension 툴을 사용했다..ㅎㅎㅎ)
자 위의 선형 방정식을 행렬 형태로 나타내 보겠다.

자 이제 이 형태에서 소거를 진행해볼 텐데 이 소거는 어떤 순으로 연산해야 할까
row 기준으로는 위부터 아래로, col기준으로 왼쪽에서 오른쪽으로 소거가 진행한다.
소거를 진행함에 있어서 다음 규칙을 지키면서 진행한다고 생각하면 된다.
Pivot을 정하고 Pivot이 있는 기준 EQ를 통해 다른 EQ의 pivot 열의 원소가 0이 되게 끔
연산이 진행된다고 생각하면 된다.
>EQ(with pivot)에 적당한 상수 배를 곱해서 제거하고자 하는 EQ에서 빼줌
우리가 가지고 있는 예시를 통해 확인해보자

의 첫행 원소 1을 기준으로 잡고 2행1열인 3을 제거해보자 !!
그럼 식은 다음과 같이 될 것이다


라는 결론을 얻게 된다.
자 그러면 다음으로는 어떻게 진행이 되어야 할까?
그렇다 Pivot으로 정한 1행1열을 기준으로 1열에는 Pivot 밑으로는 다 0이기 때문에,
다음 Pivot을 정해야 한다.
다음 피벗으로 두 번째 행으로 가보자
Pivot은 0이 될 수 없기 때문에 2행1열은 통과 다음으로 있는 두 번째 열을 보면 2가 있다.
두 번째 Pivot은 2행2열인 2가 되겠다.
if 2행2열이 0이고 3행 2열이 0이 아닌 수였다면?
row를 변환해서 적절한 pivot의 Eq(이경우 3행)랑 바꾼다. (temporary failure > row exchange)
여기서 바꿀만한 방정식이 존재하지 않는 경우 = complete failure
두 번째 pivot을 기준으로 다시 소거법을 진행해보도록 하겠다.


결과는 다음과 같다.
2행을 2배 해서 3행을 빼면 2번째 Pivot을 기준으로 밑에 원소는 0이 된다.
만약 3행이 [0 -4 4] 였다면?
연산 시 3행이 [0 0 0] 이 됨으로 not invertible(singular)이 된다.
이렇게 소거법이 끝이 나게 된다.

1행1열, 2행2열, 3행3열 = pivot
이 pivot들을 기준으로 아래 원소들이 모두 0인 상삼각 행렬(Upper triangle matrix)을 갖게 된다
(이 행렬을 U라고 부른다.)
결국 소거법의 최종 목표는 시스템 행렬(A)로부터 U를 만드는 것이다.
- Back-substitution
지금까지는 A만 고려한 소거법을 진행해 왔다 그렇지만 b까지 고려하여 소거법을 적용해야 한다
자 그럼 b까지 고려한 후방 대입[Back substitution)에 대해서 배워보겠다.
기존 행렬에서 b열을 붙인 행렬을 다음과 같이 표현되며

우리는 이 행렬을 Augmented matrix라 부른다 (추가적이 column b를 붙임 = extra column)
이 행렬을 가지고 이전에 했던 연산을 그대로 수행하면(U를 얻는 과정)

다음과 같이 U와 column c를 얻을 수 있다.
소거법을 통해 얻은 결과 식을 Ux = c 형태로 표현해보면 다음과 같다.

자 이제 후방 대입법을 통해 해를 구해보자
밑에 5z = -10 방정식부터 역순으로 풀면 미지수의 해를 얻을 수 있다.

이것이 가능한 이유는 우리가 Upper triangle 형태로 방정식을 만들었기 때문에
맨 마지막 방정식은 미지수가 하나임으로 쉽게 답을 구할 수 있게 된다.
- Elimination matrices & Matrix multiplication
앞서 소개된 소거 방법은 시스템 행렬 A와 column b에 직접 나타냈다.
이번 파트는 이를 Elimination matrix(소거 행렬)들을 행렬 A에 Matrix multiplication(행렬 곱) 과정을
통해 표현하려고 한다.
앞에 두 개념을 이해하기 앞서 저번 시간 내용에 추가하여 다음 내용을 짚고 넘어가 보자
만약 다음 행렬의 연산 관점에서 봐보자

행렬과 한 개의 Column vector를 곱을 했을 때 식이 전개되는 방식을 보면
column들의 선형 결합으로 볼 수 있다.
그러나 column의 선형 결합과 마찬가지로 Row Picture에서 보면 어떨까?
Row의 선형 결합을 표현하자면 다음과 같다.

이렇게 Row관점에서 연산되는 걸 이해해보니 위에서 다룬 소거법을
행렬로 표현할 수 있을 거 같다 한번 해봅시다
Step 1
첫 번째로 1행을 통해 2행을 소거해보는 과정을 살펴보자

행렬로 표현하면 다음과 같이 표현이 될 것이다.
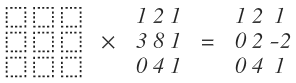
1행과 3행은 그대로 유지된다 이를 행렬로 표현하면 다음과 같이 표현될 것이다.
(한 번에 이해가 안 되는 분들은 위에 Row 선형 결합식을 통해 직접 대입해보면 이해가 편할 것이다.)
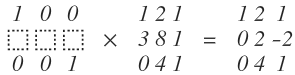
자 그럼 1행을 -3배 곱해서 2행에 더하는 과정을 표현해보자
비어있는 2행을 채우는 관점을 하나의 row벡터와 행렬을 곱하는 관점에서 보면

보이는가?
a = -3, b =1이면 될 거 같지 않은가?

이렇게 첫 번째 연산을 다음과 같이 행렬로 표현할 수 있게 됐다!

Step 2
두 번째 연산을 진행해보자.

행렬로 표현하면 다음과 같을 것이다.

위에서 구해본 짬이 있으니 이것도 쉽게 바로 구해보겠다.

쉽게 구해지는가 이게 바로 생각이 들었다면 여러분들은 제대로 이해한 것이다.
step 1을 E_21이라하고 step 2를 E_32라고 하자 (Elementary Elimination)
행렬 연산은 교환 법칙이 성립하지 않기 때문에
행렬 A에 앞으로 순차적으로 곱해져서 표현하면 될 것이다.
결합 법칙을 통해 이를 묶어서 행렬 E라고 표현한다
(one shot E single matrix elimination)

그렇지만 우리가 temporary failure 한 경우에 Row exchange를 해야 한다.
이경우 우리는 다음 행렬을 통해 이연산을 수행할 수 있는데 우리는 이 행렬을
Permutation Matrix(치환 행렬)라고 부른다.
Row exchange 관점에서 보자

Permutation P 행렬을 앞에 곱해서 1행과 2행의 위치를 바꾸고 싶은데
다음 행렬은 어떤 값을 넣으면 될까?
아마 위에 내용을 제대로 이해하셨으면 바로 답이 나올 것이다.

이렇게 출력으로 나올 행 위치에 놓을 행에 해당하는 열만 1로 설정하면 된다.
1행에 2행이 오게 하고 싶어요! = P 1행2열 = 1, 나머지 = 0
그럼 Column을 교환하고 싶을 땐 어떤 행렬을 곱해야 할까?(Column exchage)
P행렬을 우측에서 곱해주면 된다.
1열

2열
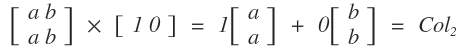
최종 결과
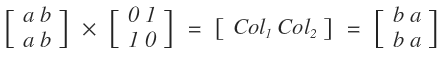
Row연산은 왼쪽, Column연산은 오른쪽 (교환 법칙[Commutative Law] 성립 X)
추가적으로 우리가 연산한 Elementary Elimination의 역행렬은 어떻게 될까요?
그리고 invertible 할까요?

쉽게 우리가 배운 1행1열을 pivot이라 두고 제거하는 관점에서
생각해보면 쉽게 답을 얻을 거라고 생각한다.
'스터디 > Linear Algebra' 카테고리의 다른 글
| [The geometry of linear equations] 선형대수 1강 (0) | 2020.11.24 |
|---|
